Математик вирішив завдання про переміщення канапи

Корейський математик презентував вирішення завдання про переміщення дивану, над яким його колеги билися з 1966 року. Він визначив максимальні розміри та форму канапи, яка пройде в коридор і не застрягне.

Про це розповідає Science Alert.

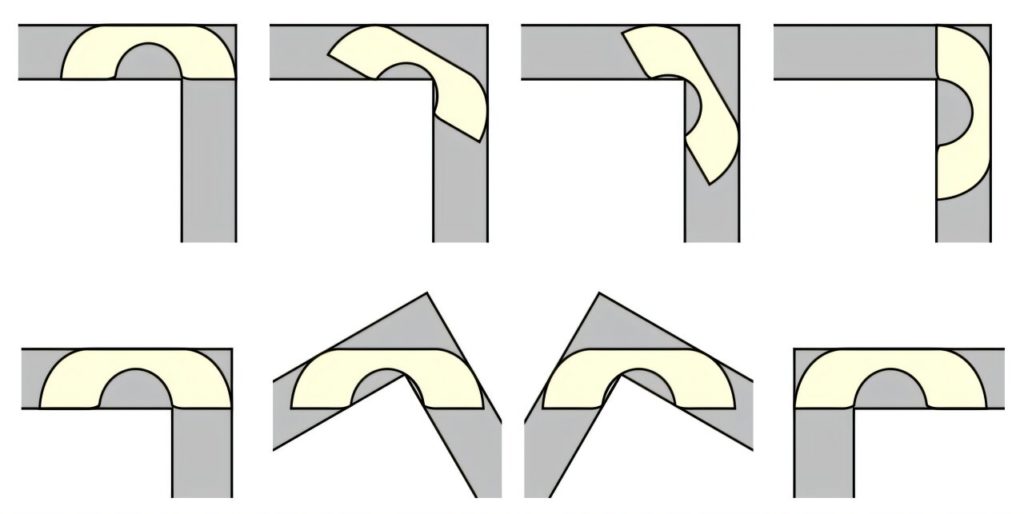
Вперше сформулював завдання канадський математик Лео Мозер: він намагався довести, що з допомогою математики можна вирішити будь-яку подібну проблему. Для цього потрібна формула площини, яку переміщують Г-подібним коридором з прямим кутом і шириною в одну одиницю. І це дозволить вирахувати максимально допустиму площу об’єкта, що подолає цей кут. Так вдасться підібрати умовний диван потрібного розміру і він не залишиться в коридорі назавжди.

Напрошувався висновок: квадратне крісло площею в одну квадратну одиницю подолає коридор досить легко, а ось такий прямокутний об’єкт, як диван з площею від двох квадратних одиниць, застрягне.

Вже за два роки після постановки питання Мозером до справи приєднався британець Джон Хаммерслі. Цей математик запропонував проносити через цей коридор диван, формою схожий на телефонну трубку. Він розрахував, що такий дизайн дозволить збільшити площу об’єкта. Останній складається з розділеного навпіл півкола з квадратом посередині і може мати площу 2,2074 одиниці.

У 1992 році вчений з Ратгерського університету (США) Джозеф Гервер згладив форми потенційного дивана – він запропонував заокруглити кілька країв за допомогою 18 дуг аналітичних кривих. Нова форма збільшила нижню межу площі до 2,2195 одиниці. Однак колеги визнали докази Гервера недостатніми, щоб стверджувати, що диван більшої площі та з іншими вигинами не пройде.

У 2018 році площа дивана була збільшена ще – до 2,37 одиниці у розрахунках математиків Йоава Каллуса з Інституту Санта-Фе та Дена Роміка з Каліфорнійського університету в Девісі.

Оскільки попередні розрахунки залишалися без переконливих доказів, за розвʼязання завдання взявся Джин-он Пек з Університету Йонсе (Південна Корея). Він опублікував свій 100-сторінковий доказ у базі препринтів arXiv.

Джин-йон Пек вибрав для демонстрації математичну конструкцію дивана Гервера. Він чітко сформулював завдання, визначив форму дивана і застосував математичні інструменти, такі, як ін’єктивна функція. У результаті розрахунків Пек дійшов такого висновку: для коридору шириною в одну одиницю максимальна площа дивану може становити 2,2195 одиниці. Таким чином, Пек довів правоту Гервера.

Розрахунок Пека тепер можна використовувати при переїздах або під час вибору нових меблів для свого житла. Звісно, ​​базові умови при цьому мають збігатися з умовами завдання. Але ще до того рішення Пека ще має пройти перевірку його колегами – так прийнято у світі математики.

Як розповідало BitukMedia, вчені з Австралії поставили під сумнів “Теорему про нескінченних мавп”. Вони дійшли висновку, що Всесвіт загине раніше, ніж мавпа встигне випадково наклацати Шекспіра на друкарській машинці. Для перевірки теорії варто було визначитися з умовами експерименту.